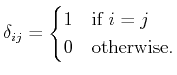Highly Nonlinear Approximations for Sparse Signal Representation

Logo EPSRC
next next up previous
Next: Elementary Definitions Up: Tutorial Previous: Tutorial

List of Symbols

The following notations and symbols will be used without defining them explicitly:
$\displaystyle \cup$ $\displaystyle :$ union  
$\displaystyle \cap$ $\displaystyle :$ intersection  
$\displaystyle \subseteq$ $\displaystyle :$ subset of  
$\displaystyle \subset$ $\displaystyle :$ proper subset of  
$\displaystyle \in$ $\displaystyle :$ belong(s)  
$\displaystyle \mathbb{N}$ $\displaystyle :$ set of all positive integers  
$\displaystyle \mathbb{Z}$ $\displaystyle :$ set of all integers  
$\displaystyle \mathbb{R}$ $\displaystyle :$ field of all real numbers  
$\displaystyle \mathbb{C}$ $\displaystyle :$ field of all complex numbers  
$\displaystyle \mathbb{F}$ $\displaystyle :$ field of real or complex numbers  
$\displaystyle :=$ $\displaystyle :$ is defined by  
$\displaystyle \Longrightarrow$ $\displaystyle :$ imply (implies)  
$\displaystyle \Longleftrightarrow$ $\displaystyle :$ if and only if  
$\displaystyle \to$ $\displaystyle :$ maps to  

The Kronecker symbol is given by

$\displaystyle \delta_{ij}=\begin{cases}1 & \text{if $i=j$}\\ 0 & \text{otherwise.} \end{cases} $

The characteristic function $ \chi_S$ of a set $ S$ is defined as

$\displaystyle \chi_S(x)=\begin{cases}1 & \text{if $ x\in S$}\\ 0 & \text{otherwise.} \end{cases} $

For $ n\in \mathbb{N}$ the factorial $ n!$ is defined as $ n!=n(n-1)\cdots 2\cdot1.$ The absolute value of a number $ a \in \mathbb{F}$ is indicated as $ \vert a\vert$. If $ a\in \mathbb{R}$

$\displaystyle \vert a\vert=\begin{cases}a & \text{if $a \ge 0$}\\ -a & \text{if $a < 0$}. \end{cases} $

If $ a \in \mathbb{C}$ its complex conjugate is denoted by $ \overline {a}$ and $ \vert a\vert^2=a \overline {a}.$

next next up previous
Next: Elementary Definitions Up: Tutorial Previous: Tutorial