Highly Nonlinear Approximations for Sparse Signal Representation
The spaces
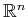 ,
, ![$ L^2[a,b]$](img122.png) and
and ![$ C^k[a,b]$](img123.png)
The Euclidean space
![]() is an inner product space with
inner product defined by
is an inner product space with
inner product defined by
The space ![]() is an inner product space of
functions on
is an inner product space of
functions on ![]() with
inner product defined by
with
inner product defined by
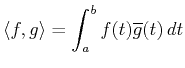
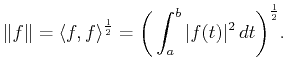
The space ![]() is the space of functions on
is the space of functions on ![]() having continuous derivatives up to order
having continuous derivatives up to order
![]() .
The space of continuous functions on
.
The space of continuous functions on ![]() is denoted as
is denoted as ![]() .
.

