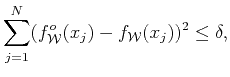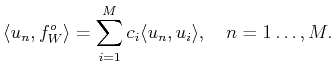Without loss of generality we assume here that the
measurements on the signal in hand are given by the
values the signal takes at the sampling points
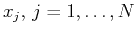
.
Thus, the measures are obtained from
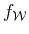
as
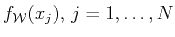
and
the functionals
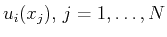
from vectors
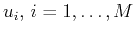
. Since the values
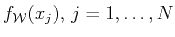
arise from observations or experiments they are usually affected by
errors therefore we use the notation
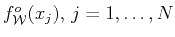
for the observed data and request that the model
given by the r.h.s. of (
29)
satisfies the restriction
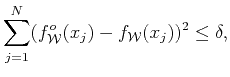 |
(30) |
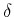
accounting for the data's error.
Nevertheless, rather than using directly this restriction as
constraints of the
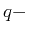
norm
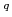
we handle the available information
using an idea introduced much earlier, in [
19], and
applied in [
20] for transforming the constraint (
30)
into linear equality constraints.
Replacing
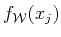
by (
29), the condition of minimal square distance
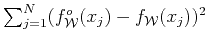
leads to the so called
normal equations:
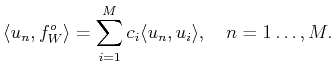 |
(31) |
Of course, since we are concerned with ill posed problems
we cannot use all these equations to find the coefficients
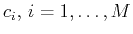
. However, as proposed in [
19],
we could use `some'
of these equations as constraints of our optimization process.
The number of such equations being the necessary to reach the condition
(
30).
We have then transformed the original problem into the one of minimizing
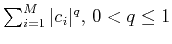
, subject to a number of
equations selected from
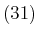
, the
-th
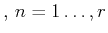
ones say.
In line with [
19] we select the subset of equations (
31) in
an iterative fashion. We start by the initial estimation
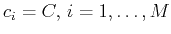
, where the constant
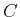
is determined by
minimizing the distant between the model and the data. Thus,
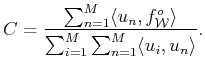 |
(32) |
With this initial estimation we `predict' the normal equations
(
31) and select as our first constraint the worst predicted
by the initial solution, let this equation be the
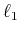
-th one. We then minimize
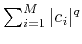
subject to the constraint
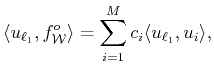 |
(33) |
and indicate the resulting coefficients as
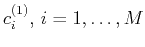
. With
these coefficients we predict equations (
31) and select
the worst predicted as a new constraint to obtain
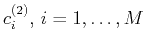
and so on.
The iterative process is stopped when the condition
(
30) is reached.
The numerical example discussed next has been solved by recourse to the method for minimization of the  -norm)
-norm) published in
[16]. Such an iterative method, called FOCal Underdetermined
System Solver (FOCUSS) in that publication,
is straightforward implementable. It
evolves by computation of pseudoinverse matrices, which
under the given hypothesis of our problem, and within
our recursive strategy for feeding the constraints,
are guaranteed to be numerically stable
(for a detailed explanation of the method see [16]).
The routine for implementing the proposed strategy
is ALQMin.m.
published in
[16]. Such an iterative method, called FOCal Underdetermined
System Solver (FOCUSS) in that publication,
is straightforward implementable. It
evolves by computation of pseudoinverse matrices, which
under the given hypothesis of our problem, and within
our recursive strategy for feeding the constraints,
are guaranteed to be numerically stable
(for a detailed explanation of the method see [16]).
The routine for implementing the proposed strategy
is ALQMin.m.
Subsections
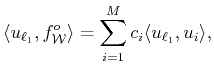
![]() -norm)
-norm)![]() published in
[16]. Such an iterative method, called FOCal Underdetermined
System Solver (FOCUSS) in that publication,
is straightforward implementable. It
evolves by computation of pseudoinverse matrices, which
under the given hypothesis of our problem, and within
our recursive strategy for feeding the constraints,
are guaranteed to be numerically stable
(for a detailed explanation of the method see [16]).
The routine for implementing the proposed strategy
is ALQMin.m.
published in
[16]. Such an iterative method, called FOCal Underdetermined
System Solver (FOCUSS) in that publication,
is straightforward implementable. It
evolves by computation of pseudoinverse matrices, which
under the given hypothesis of our problem, and within
our recursive strategy for feeding the constraints,
are guaranteed to be numerically stable
(for a detailed explanation of the method see [16]).
The routine for implementing the proposed strategy
is ALQMin.m.