Highly Nonlinear Approximations for Sparse Signal Representation

Logo EPSRC
next next up previous
Next: Subspaces - Direct sum Up: Elementary Definitions Previous: Elementary Definitions

Vector Space

A vector space over a field $ \mathbb{F}$ is a set $ {\cal{V}}$ together with two operations vector addition, denoted $ v + w \in {\cal{V}}$ for $ v,w\in {\cal{V}}$ and scalar multiplication, denoted $ av \in {\cal{V}}$ for $ a \in \mathbb{F}$ and $ v \in {\cal{V}}$, such that the following axioms are satisfied:

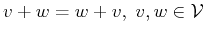  1. $ v+w=w+v,\; v,w \in {\cal{V}}$.
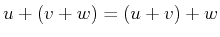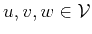  2. $ u + (v + w) = (u+v) + w$, $ u,v,w \in {\cal{V}}$.
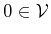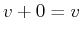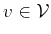  3. There exists an element $ 0 \in {\cal{V}}$, called the zero vector, such that $ v+0 = v$, $ v \in {\cal{V}}$.
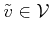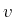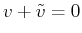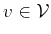  4. There exists an element $ \tilde {v} \in {\cal{V}}$, called the additive inverse of $ v$, such that $ v + \tilde {v}= 0$, $ v \in {\cal{V}}$.
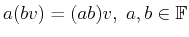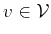  5. $ a(bv) = (ab)v,\; a,b \in \mathbb{F}$ and $ v \in {\cal{V}}$.
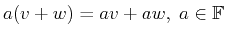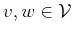  6. $ a(v+w) = av + aw,\; a \in \mathbb{F}$ and $ v,w\in {\cal{V}}$.
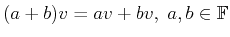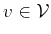  7. $ (a+b)v = av + bv,\; a,b \in \mathbb{F}$ and $ v \in {\cal{V}}$.
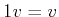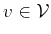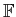  8. $ 1v=v$, $ v \in {\cal{V}}$, where 1 denotes the multiplicative identity in $ \mathbb{F}$.
The elements of a vector space are called vectors.