Highly Nonlinear Approximations for Sparse Signal Representation
Background and notations
We refer to the fundamental books [23,25] for a complete treatment of splines. Here we simply introduce the notation and basic definitions which are needed in the present context.
Definition 1
Given a finite closed interval ![$ [c,d]$](img495.png) we define
a partition of
we define
a partition of ![$ [c,d]$](img495.png) as the finite set of points
as the finite set of points
We further define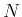 subintervals
subintervals
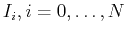 as:
as:
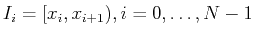 and
and
![$ I_N=[x_N,x_{N+1}]$](img500.png) .
.
We further define
Definition 2
Let 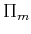 be the
space of polynomials of
degree smaller than or equal to
be the
space of polynomials of
degree smaller than or equal to
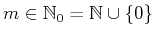 ,
i.e.,
,
i.e.,
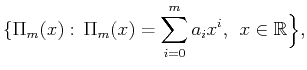 and define
and define
where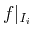 indicates the
restriction of the function
indicates the
restriction of the function 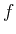 on the
interval
on the
interval 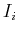 .
.
The construction of nonuniform dictionaries arises from the
next proposition [21]
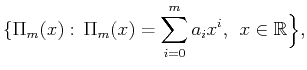
| (35) |
where
Theorem 1
Suppose that
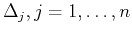 are partitions of
are partitions of ![$ [c,d]$](img495.png) .
Then
.
Then