Application to Image Folding

In order to apply the embedding scheme to fold an image we simply process the image by dividing it into, say

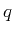
blocks,

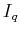
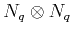
of $N_q\otimes N_q$ pixels. We find the representation of each block with a combination of discrete cosine and spline based subdictionaries constructed as explained in [35]. With this dictionaries the image of Fig 10 has a highly sparse representation at PSNR=40 dB (the CR is approximately 11) so that we are able to store the whole image embedding the few pixels shown in the top picture of Fig 10. The next picture is the unfolded image without using the security key and the right picture the one obtained with the correct key. For further implementation details see [33]. An example of how to call the available codes for sparse image approximation with cosine and spline based dictionaries can be found here.

**Figure 10:** The small picture at the top is the folded Image. The left picture below is the unfolded image without knowledge of the private key to initialize the permutation. The next is the unfolded picture when the correct key is used.
$\includegraphics[width=6cm]{lena_folded.eps}$

Highly Nonlinear Approximations for Sparse Signal Representation

Application to Image Folding