Highly Nonlinear Approximations for Sparse Signal Representation
Normed vector space
A norm ![]() on a vector space
on a vector space ![]() is a function from
is a function from
![]() to
to
![]() such that for every
such that for every
![]() and
and
![]() the
following three properties are fulfilled
the
following three properties are fulfilled
-
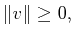 and
and
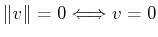 .
.
-
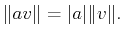
-
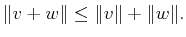
A norm ![]() on a vector space
on a vector space ![]() is a function from
is a function from
![]() to
to
![]() such that for every
such that for every
![]() and
and
![]() the
following three properties are fulfilled
the
following three properties are fulfilled