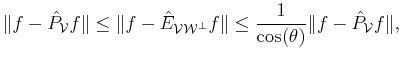Highly Nonlinear Approximations for Sparse Signal Representation

Logo EPSRC
next next up previous
Next: Example 2 Up: Oblique and Orthogonal Projector Previous: Oblique and Orthogonal Projector

Example 1

Let us assume that the signal processing task is to approximate a signal $ f\in \cal{H}$ by a signal $ f_{{\cal{V}}}\in {\cal{V}}$. In this case, one normally would choose $ f_{{\cal{V}}} = \hat{P}_{{\cal{V}}}f$ because this is the unique signal in $ {{\cal{V}}}$ minimizing the distance $ \Vert f - f_{{\cal{V}}}\Vert$. Indeed, let us take another signal $ g$ in $ {\cal{V}}$ and write it as $ g= g+ \hat{P}_{{\cal{V}}}f - \hat{P}_{{\cal{V}}}f$. Since $ f-\hat{P}_{{\cal{V}}}f$ is orthogonal to every signal in $ {\cal{V}}$ we have

$\displaystyle \Vert f - g\Vert^2 = \Vert f - g+ \hat{P}_{{\cal{V}}}f - \hat{P}_... ... \Vert f - \hat{P}_{{\cal{V}}}f\Vert^2 + \Vert \hat{P}_{{\cal{V}}}f - g\Vert^2.$

Hence $ \Vert f - g\Vert$ is minimized if $ g= \hat{P}_{{\cal{V}}}f$.

Remark 1   Any other projection would yield a distance 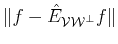$ \Vert f - \hat{E}_{{\cal{V}}{\cal{W}^\bot}}f\Vert$ which satisfies [2]

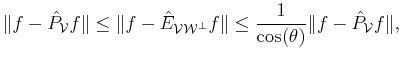$\displaystyle \Vert f - \hat{P}_{\cal{V}}f\Vert \le \Vert f - \hat{E}_{{\cal{V}... ...{W}^\bot}}f\Vert \le \frac{1}{\cos(\theta)} \Vert f - \hat{P}_{\cal{V}}f\Vert,$

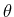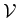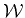where $ \theta$ is the minimum angle between the subspaces $ {\cal{V}}$ and $ {\cal{W}}$. The equality is attained for 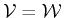$ {\cal{V}}= {\cal{W}}$, which corresponds to the orthogonal projection.