Example 2

Assume that the signal

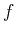
to be analyzed here is the superposition of two signals,

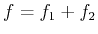
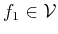
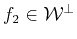
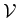
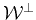
, each component being produced by a different phenomenon we want to discriminate. Let us assume further that $f_1 \in {\cal{V}}$ and $f_2 \in {\cal{W}^\bot}$ with ${\cal{V}}$ and ${\cal{W}^\bot}$ disjoint subspaces. Thus, we can obtain,

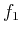
say, from

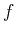
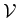
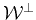
, by an oblique projector onto ${\cal{V}}$ and along ${\cal{W}^\bot}$ . The projector will map to zero the component

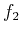
to produce

$\displaystyle f_1= \hat{E}_{{\cal{V}}{\cal{W}^\bot}} f.$

Highly Nonlinear Approximations for Sparse Signal Representation

Example 2