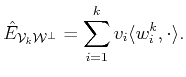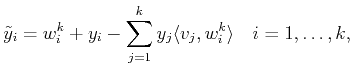Highly Nonlinear Approximations for Sparse Signal Representation
Updating the oblique projector
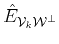 to
to
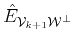
We assume that
In order to inductively construct the duals
- i)
-
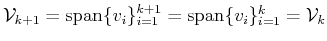 ,
i.e.,
,
i.e.,
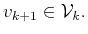
- ii)
-
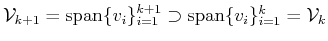 , i.e.
, i.e.
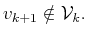
Case i)
Proposition 4
Let
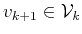 and vectors
and vectors 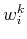 in (17) be given. For an arbitrary vector
in (17) be given. For an arbitrary vector
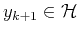 the dual vectors
the dual vectors 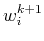 computed as
computed as
for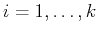 and
and
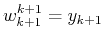 produce the identical oblique projector as the dual vectors
produce the identical oblique projector as the dual vectors
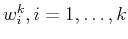 .
.
for
Case ii)
Proposition 5
Let vector
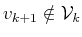 and vectors
and vectors
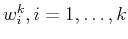 in (17) be given. Thus
the dual vectors
in (17) be given. Thus
the dual vectors 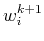 computed as
computed as
where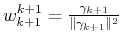 with
with
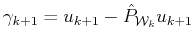 ,
provide us with the oblique projector
,
provide us with the oblique projector
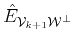 .
.
The proof these propositions are given in [10].
The codes for updating the dual vectors are
FrInsert.m
and FrInsertBlock.m.
where
Property 2
If vectors
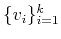 are linearly independent
they are also biorthogonal to the dual
vectors arising inductively from
the recursive equation (19).
are linearly independent
they are also biorthogonal to the dual
vectors arising inductively from
the recursive equation (19).
The proof of this property is in [10].