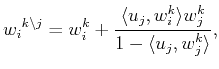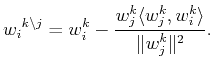Highly Nonlinear Approximations for Sparse Signal Representation
Downdating the oblique projector
 to
to
Let us suppose that by the elimination of
the element - i)
-
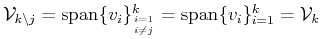 i.e.,
i.e.,
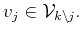
- ii)
-
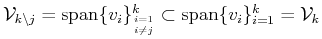 , i.e.,
, i.e.,
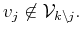
Case i)
Proposition 6
Let
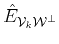 be given by (17) and let us assume
that removing vector
be given by (17) and let us assume
that removing vector 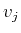 from the spanning set of
from the spanning set of
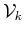 leaves the identical subspace, i.e.,
leaves the identical subspace, i.e.,
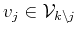 .
Hence, if the remaining dual vectors are
modified as follows:
.
Hence, if the remaining dual vectors are
modified as follows:
the corresponding oblique projector does not change, i.e.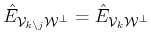 .
.
the corresponding oblique projector does not change, i.e.
Case ii)
Proposition 7
Let
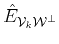 be given by (17) and let us assume
that the vector
be given by (17) and let us assume
that the vector 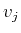 to be removed from the spanning
set of
to be removed from the spanning
set of
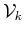 is not in
is not in
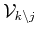 .
In order to produce the oblique projector
.
In order to produce the oblique projector
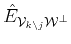 the
appropriate modification of the dual vectors can be achieved
by means of the following equation
the
appropriate modification of the dual vectors can be achieved
by means of the following equation
The proof these propositions are given in [10]. The code for updating the vectors are FrDelete.m.