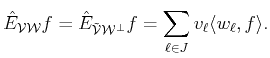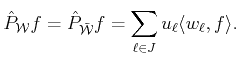Highly Nonlinear Approximations for Sparse Signal Representation

• Project Overview
• Tutorial [.ps | .pdf]
• Source code
• Examples
• Publications
• EIFS
• SCEIFS
• Acknowledgements

• Home
• maths@Aston
• EPSRC Home

Signals discrimination by subspace selection

We discuss now the possibility of extracting the signal $f_{\cal{V}}$, from a mixture $f= f_{\cal{V}}+ f_{\cal{V}}$ when the subspaces ${\cal{V}}$ and ${\cal{W}^\bot}$ are not well separated and the oblique projector onto ${\cal{V}}$ along ${\cal{W}^\bot}$ fails to yield the right signals separation. For this we introduce the following hypothesis on the class of signals to be considered:

We assume that the signal of interest is $K$-sparse in a spanning set for ${\cal{V}}$

This implies that given $\{v_i\}_{i=1}^M$ there exists a subset of elements characterized by the set of indices ${J}$, of cardinality $K < M$, spanning the subspace ${\cal{\tilde {V}}}= {\mbox{\rm {span}}}\{v_\ell\}_{\ell \in J}$ and such that $f_{\cal{V}}= \hat{E}_{{\cal{\tilde {V}}}{\cal{W}^\bot}} f.$ Thus, the hypothesis generates an, in general, intractable problem because the number of possible subspaces spanned by $K$ vectors out of $M$ is a combinatorial number $\tbinom{M}{K} =\frac{{M!}}{(M-K)!K!}$.

The techniques developed within the project aim at reducing complexity by making the search for the right subspace signal dependent.

Given a signal $f$, and assuming that the subspaces ${\cal{W}^\bot}$ and ${\cal{V}}= {\mbox{\rm {span}}}\{v_i\}_{i=1}^M$, are known, the goal is to find $\{v_\ell\}_{\ell \in J} \subset \{v_i\}_{i=1}^M$ spanning ${\cal{\tilde {V}}}$ and such that $\hat{E}_{{\cal{\tilde {V}}}{\cal{W}^\bot}} f= \hat{E}_{{\cal{V}}{\cal{W}^\bot}} f$. The cardinality of the subset of indices $J$ should be such that construction of $\hat{E}_{{\cal{\tilde {V}}}{\cal{W}^\bot}}$ is well posed. This assumption characterizes the class of signals that can be handled by the proposed approaches.

Under the stated hypothesis, if the subspace ${\cal{\tilde {V}}}$ were known, one would have

$$\hat{E}_{{\cal{V}}{\cal{W}}} f= \hat{E}_{{\cal{\tilde {V}}}{\cal{W}^\bot}} f = \sum_{\ell \in J} v_{\ell} \langle w_{\ell}, f\rangle .$$ (23)

However, if the computation of $\hat{E}_{{\cal{V}}{\cal{W}^\bot}}$ is an ill posed problem, which is the situation we are considering, $\hat{E}_{{\cal{V}}{\cal{W}^\bot}} f$ is not available. In order to look for the subset of indices $J$ yielding ${{\cal{\tilde {V}}}}$ one may proceed as follows: Applying $\hat{P}_{\cal{W}}$ on every term of (23) and using the properties $\hat{P}_{\cal{W}}\hat{E}_{{\cal{V}}{\cal{W}^\bot}}= \hat{P}_{\cal{W}}$ and $\hat{P}_{\cal{W}}\hat{E}_{{\cal{\tilde {V}}}{\cal{W}^\bot}}= \hat{P}_{\cal{\tilde {W}}}$, where ${\cal{\tilde {W}}}= {\mbox{\rm {span}}}\{u_{\ell}\}_{\ell \in J}$, (23) becomes

$$\hat{P}_{\cal{W}}f= \hat{P}_{\cal{\tilde {W}}}f = \sum_{\ell \in J} u_{\ell} \langle w_{\ell}, f\rangle .$$ (24)

Since ${\cal{W}^\bot}$ is given and $\hat{P}_{\cal{W}}f= f - \hat{P}_{\cal{W}^\bot}f$, the left hand side of (23) is available and we can search for the set $\{u_{\ell}\}_{\ell \in J} \subset \{u_i\}_{i=1}^M$, in a stepwise manner by adaptive pursuit approaches.

This project is supported by EPSRC (EP/D062632/1)