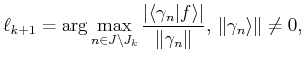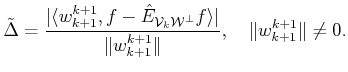Highly Nonlinear Approximations for Sparse Signal Representation
Oblique Matching Pursuit (OBMP)
The criterion we use for the forward recursive selection of the set
By fixing
![]() , at iteration
, at iteration ![]() we select the index
we select the index
![]() such that
such that
![]() is minimized.
is minimized.
Proposition 8
Let us denote by 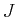 the set of indices
the set of indices
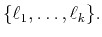 Given
Given
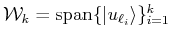 ,
the index
,
the index
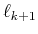 corresponding to the atom
corresponding to the atom
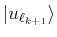 for which
for which
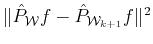 is minimal
is to be determined as
is minimal
is to be determined as
with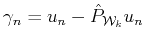 and
and 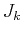 the set of indices that have been previously
chosen to determine
the set of indices that have been previously
chosen to determine
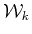 .
.
with
Proof.
It readily follows since
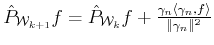 and hence
and hence
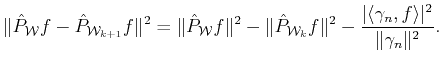 Because
Because
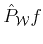 and
and
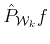 are
fixed,
are
fixed,
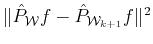 is minimized if
is minimized if
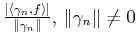 is maximal over all
is maximal over all
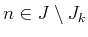 .
.

The original OBMP selection criterion
proposed in [11]
selects the index
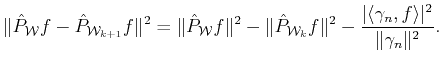
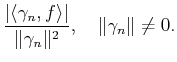
In order to cancel this error, the new approximation is constructed accounting for the concomitant measurement vector.
Proof.
Since for all vector
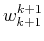 given in
(19)
given in
(19)
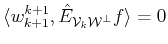 and
and
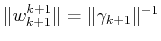 we have
we have
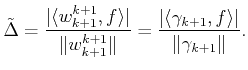 Hence, maximization of
Hence, maximization of
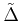 over
over
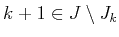 is equivalent to (25).
is equivalent to (25).

It is clear at this point that the forward selection of
indices prescribed by proposition (25) is equivalent to
selecting the indices by applying OOMP [12] on the projected signal
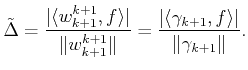
![[*]](crossref.png) .
.