Highly Nonlinear Approximations for Sparse Signal Representation
Implementing corrections
Let us discuss now the possibility of correcting bad moves in the forward selection, which is specially necessary when dealing with ill posed problems. Indeed, assume we are trying to approximate a signal which is
Consider that at iteration ![]() the correct subspace has not
appeared yet and the selected indices are labeled by the
the correct subspace has not
appeared yet and the selected indices are labeled by the ![]() indices
indices
![]() .
In order to choose the index of the atom that
minimizes the norm of the residual error as passing
from approximation
.
In order to choose the index of the atom that
minimizes the norm of the residual error as passing
from approximation
![]() to approximation
to approximation
![]() we should fix the index of the atom to be deleted,
we should fix the index of the atom to be deleted, ![]() say,
as the one for which the quantity
say,
as the one for which the quantity
is minimized [13,14].
The process of eliminating one atom from the atomic decomposition
is called backward step while the process of
adding one atom is called forward step.
The forward selection criterion to choose the atom to replace the
one eliminated in the previous step is accomplished by
finding the index
![]() for which
the functional
for which
the functional
is maximized. In our framework, using (22), the projector
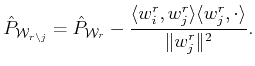

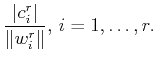
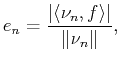 with
with