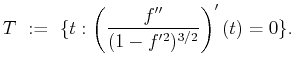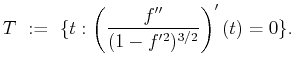Given a signal,
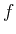
say, we address now the issue of determining a
partition

, and sub-partitions
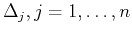
,
such that: a)
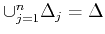
and b) the partitions are
suitable for generating a sparse representation of the
signal in hand. As a first step we propose to tailor the partition
to the signal
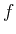
by setting

taking into account
the critical points of the curvature function
of the signal, i.e.,
Usually the entries in
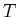
are chosen as the initial knots of

. In order to obtain more knots we apply subdivision
between consecutive knots in
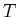
thereby obtaining a partition

with the decided number of knots. An algorithm for
implementing such procedure can be found in [
21].
According to Theorem
2, in order to build a dictionary
for
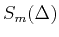
we need to choose
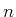
-subpartitions
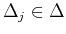
such that
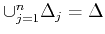
. As an
example we suggest a simple method for producing
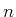
-subpartitions
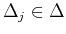
, which is used in the numerical simulations of
the next section. Considering the partition
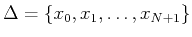
such that

, for each integer
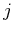
in
![$ [1,n]$](img549.png)
we set
![$\displaystyle \Delta _j := \{c,d\}\cup \{x_{k} : k\in [1,N]$](img550.png)
and
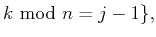
e.g. if
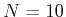
and
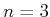
, we have
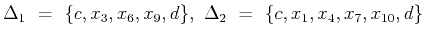

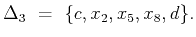
The codes for creating a partition adapted to a given
signal are
ProducePartition.m
and
FinalProducePartition.m
and
the one code for creating the dictionaries for the space is
CutDic.m.
Subsections