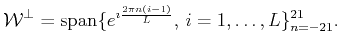Application to filtering low frequency noise from a seismic signal

A common interference with broadband seismic signals is produced by long waves, generated by known or unknown sources, called infragravity waves [28,29,30]. Such an interference is refereed to as low frequency noise, because it falls in a frequency range of up to 0.05 Hz. Thus, in [31] we consider that the model of the subspace of this type of structured noise, on a signal given by

samples, is

$\displaystyle {\cal{W}^\bot}= {\mbox{\rm {span}}}\{e^{\imath \frac{2\pi n(i-1)}{L}}, i=1,\ldots,L\}_{n=-21}^{21}.$

(36)

The particular realization of the noise we have simulated is plotted in the left graph of Fig 9. However, the success of correct filtering does not depend on the actual form of the noise (as long as it belongs to the subspace given in (36)) because the approach we consider guarantees the suppression of the whole subspace ${\cal{W}^\bot}$ . The seismic signal to be discriminated from the noisy one is a piece of the signal in the right graph of Fig 8. The middle graph in Fig 9 depicts the signal

which is formed by adding both components. Constructing $\hat{P}_{\cal{W}^\bot}$ we obtain $f_{{\cal{W}}}=f - \hat{P}_{\cal{W}^\bot}f$ and use the routine ProducePartition.m to find a partition adapted to this projection. In this case, to succeed in modelling a signal subspace complementary to ${\cal{W}^\bot}$ we needed a basis for the nonuniform spline space and a regularized version of the FOCUSS algorithm [32]. The result is plotted in the right graph of Fig 9. The implementation details can be found in [31].

**Figure 9:** Simulated low frequency noise (left) Signal plus noise (middle) Approximation recovered from the middle graph as explained in [31]
$\includegraphics[width=5.6cm]{infrawave.eps}$ $\includegraphics[width=5.6cm]{compo.eps}$ $\includegraphics[width=5.6cm]{seismic_ap.eps}$

Highly Nonlinear Approximations for Sparse Signal Representation

Application to filtering low frequency noise from a seismic signal