Highly Nonlinear Approximations for Sparse Signal Representation

Logo EPSRC
next next up previous
Next: Application to filtering low Up: Application to sparse signal Previous: Application to sparse signal

Numerical examples

We produce here an example illustrating the potentiality of the proposed nonuniform dictionaries for achieving sparse representations by nonlinear techniques. The signals we consider are the chirp signal $ f_1$ and the seismic signal $ f_2$ plotted in the Fig. 8.

Figure 8: Chirp signal $ f_1$ (left). Seismic signal $ f_2$ (right).
\includegraphics[width=8cm]{ff_1.eps} \includegraphics[width=8cm]{ff_2.eps}

We deal with the chirp signal $ f_1$ on the interval $ [0,8]$, by discretizing it into $ L=2049$ samples and applying Algorithm 1 to produce the partition. The resulting number of knots is $ 1162$, which is enough to approximate the signal, by a cubic B-spline basis for the space, within the precision $ {\rm {tol}_1= 0.01 \Vert f_1 \Vert}$. A dictionary $ {\mathcal {D}}_4(\Delta : \cup_{j=1}^{10}\Delta _j)$ for the identical space is constructed by considering 10 subpartitions, which yield $ N_1=1200$ functions.

The signal $ f_2$ is a piece of $ L=513$ data. A partition of cardinality $ 511$ is obtained as $ \Delta = T(f_1,8)$ and the dictionary of cubic splines we have used arises by considering $ 3$ subpartitions, which yields a dictionary $ {\mathcal D}_4(\Delta : \cup_{j=1}^{3}\Delta _j)$ of cardinality $ N_2= 521$.

Denoting by $ \alpha^i_n, n=1,\ldots,N_i$ the atoms of the $ i$th-dictionary, we look now for the subsets of indices $ \Gamma_i, i=1,2$ of cardinality $ K_i, i=1,2$ providing us with a sparse representation of the signals. In other words, we are interested in the approximations

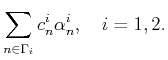$\displaystyle f_i^{K_i}$ $\displaystyle =$ $\displaystyle \sum_{n\in\Gamma_i} c_n^i \alpha^i_n,\quad i=1,2.$  

such that $ \Vert f_i^{K_i} - f_i\Vert \le {\rm {tol}}_i, i=1,2$ and the values $ K_i, i=1,2$ are satisfactory small for the approximation to be considered sparse. Since the problem of finding the sparsest solution is intractable, for all the signals we look for a satisfactory sparse representation using the same greedy strategy, which evolves by selecting atoms through stepwise minimization of the residual error as follows.
i)
The atoms are selected one by one according to the Optimized Orthogonal Matching Pursuit (OOMP) method [12] until the above defined tolerance for the norm of the residual error is reached.
ii)
The previous approximation is improved, without greatly increasing the computational cost, by a `swapping refinement' which at each step interchanges one atom of the atomic decomposition with a dictionary atom, provided that the operation decreases the norm of the residual error [13].
iii)
A Backward-Optimized Orthogonal Matching Pursuit (BOOMP) method [14] is applied to disregard some coefficients of the atomic decomposition, in order to produce an approximation up to the error of stage i). The last two steps are repeated until no further swapping is possible. The routine implementing the steps is OOMPFinalRefi.m.

The described technique is applied to all the non-orthogonal dictionaries we have considered for comparison with the proposed approach. The results are shown in Table 1. In the first column we place the dictionaries to be compared. These are: 1) the spline basis for the space adapted to the corresponding signal. 2) The dictionary for the identical spaces consisting of functions of larger support. 3) The orthogonal cosine bases used by the discrete cosine transform (dct). 4) The semi-orthogonal cardinal Chui-Wang spline wavelet basis [26] and 5) the Chui-Wang cardinal spline dictionary for the same space [27].



Table 1: Comparison of sparsity performance achieved by selecting atoms from the non-uniform bases and dictionaries for adapted spline space (1st and 2nd rows), dft (3rd row), cardinal wavelet bases and dictionaries (4th and 5th rows).
Dictionaries $ K^1$ (signal $ f_1$) $ K^2$ (signal $ f_2$)
Non-uniform spline basis 1097 322
Non-uniform spline dictionary 173 129
Discreet cosine transform 263 208
Cardinal Chui-Wang wavelet basis 246 201
Cardinal Chui-Wang wavelet dictionary 174 112

Notice that whilst the non-uniform spline space is adapted to the corresponding signal, only the dictionary for the space achieves the sparse representation. Moreover the performance is superior to that of the Chui-Wang spline wavelet basis [26] and similar to the cardinal Chui-Wang dictionary, which is known to render a very good representation for these signals [27]. However, whilst the Chui-Wang cardinal spline wavelet dictionaries introduced in [27] are significantly redundant with respect to the corresponding basis (about twice as larger) the non-uniform B-spline dictionaries introduced here contain a few more functions than the basis. Nevertheless, as the examples indicate, the improvement in the sparseness of the approximation a dictionary may yield with respect to the B-spline basis is enormous.
next next up previous
Next: Application to filtering low Up: Application to sparse signal Previous: Application to sparse signal